Circulation
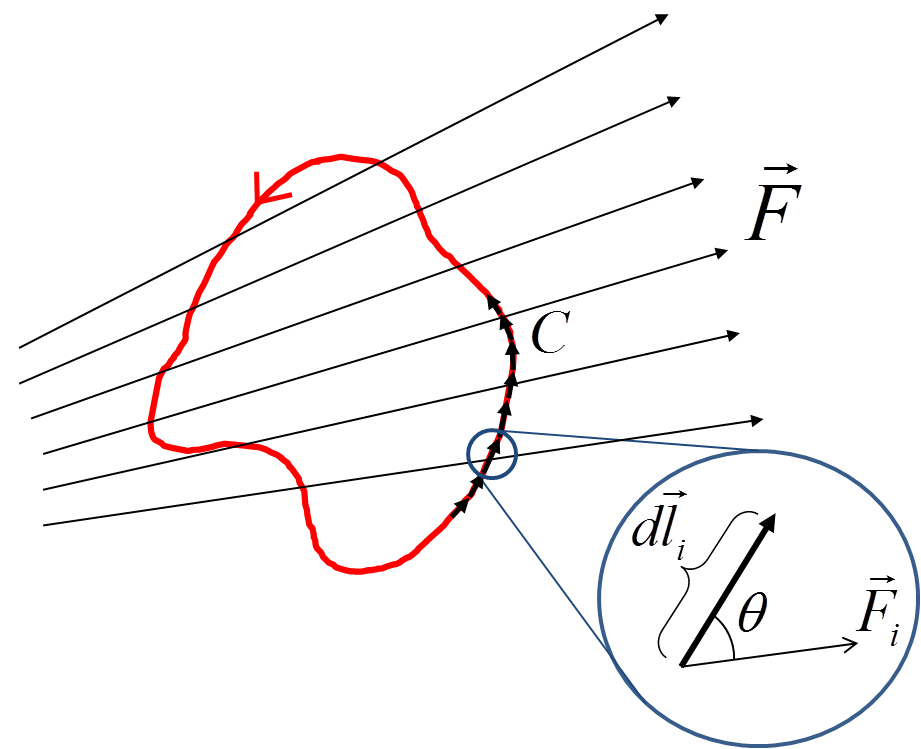
Before we can move onto our third and final operation with del, we need to be introduced to the mathematical concept of circulation. We know work done is defined by \( \mathrm{force} \times \mathrm{distance} \) where the distance moved is in the direction of the force.
If the force \( \vec{F} \) is constant and in the same direction as the displacement \( \vec{l} \), then the work \( W \) is given by $$ W = \vert \vec{F} \vert \vert \vec{l} \vert $$ If the force is constant but at an angle \( \theta \) to the displacement, $$ W = \vert \vec{F} \vert \vert \vec{l} \vert \cos\theta = \vec{F} \circ \vec{l} $$ If the force is not constant, and the angle between the force and displacement varies along the path, then we need to consider the path as being comrpised of infinitesimal displacements \( d\vec{l} \), $$ dW = \vert \vec{F} \vert \vert d\vec{l} \vert \cos\theta = \vec{F} \circ d\vec{l} \nonumber $$ Now let's add up all these to find the total work done in moving along the path, $$ W = \int_C \vec{F} \circ d\vec{l} $$
The subscript \( C \) reminds us that it is a line integral along the path \( C \).
The circulation is when we evaluate the work done around a closed loop where the start and end points are at the same location. The direction of integration is anti-clockwise by convention. $$ \mathrm{Circulation} = \oint_C \vec{F} \circ d\vec{l} $$ This operation can be thought of as how much the field follows the path \( C \) that we take.