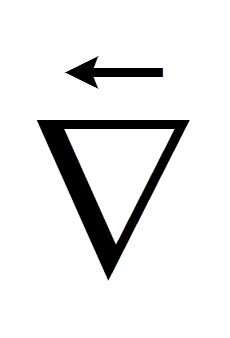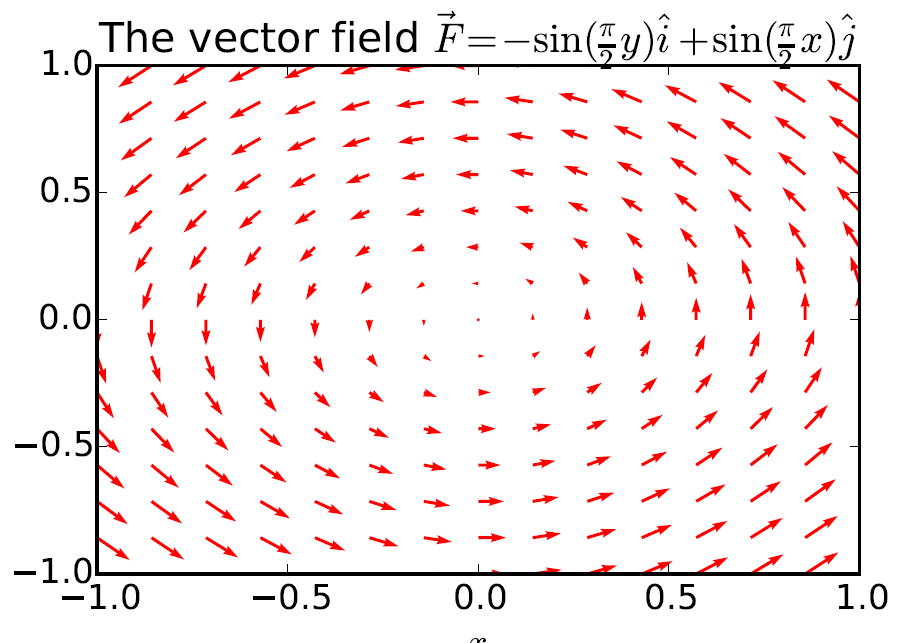
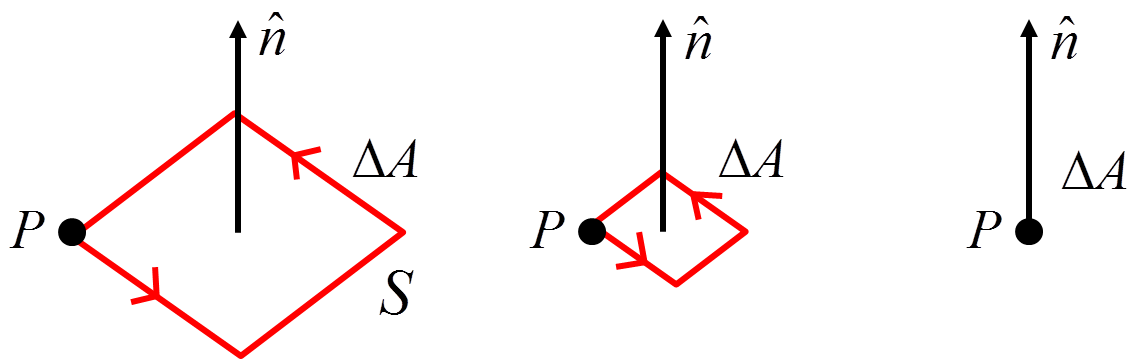
CurlVector fields such as the one shown below appear to circulate. We want to find an operation which takes a vector field \( \vec{E} \) and produces another vector field \( \mathrm{curl}(\vec{E}) \) which tells us at every location how much the field rotates and in which direction. |
|
|
|
|
|
We saw previously that the circulation can be thought of as how much the field moves around an area, but we want to work out how much it rotates about a point. How do we do this? As our operation produces a vector field we must calculate each component separately. We define the \( \hat{n} \) component of the curl which is in a direction normal to a surface \( \Delta A \) as the ratio of the circulation around a closed loop \( S \) to the area \( \Delta A \) that the loop encloses. Then we let this area tend to zero down to a point.
$$ \mathrm{curl}(\vec{E}) \circ \hat{n} \equiv \lim_{\Delta A \rightarrow 0} \frac{\mathrm{circulation}}{\Delta A} = \lim_{\Delta A \rightarrow 0} \frac{1}{\Delta A} \oint _C \vec{E} \circ d\vec{l}$$
We dot our curl vector field with \( \hat{n} \) as it brings out the \( \hat{n} \) component of the curl. | |
|
|
|
|
