Almost there...
Here is the definition of the curl in the \( \hat{n} \) direction. We shall use this definition to derive an operation to find the curl!
$$ \mathrm{curl}(\vec{E}) \circ \hat{n} \equiv \lim_{\Delta A \rightarrow 0} \frac{\mathrm{circulation}}{\Delta A} = \lim_{\Delta A \rightarrow 0} \frac{1}{\Delta A} \oint _C \vec{E} \circ d\vec{l}$$
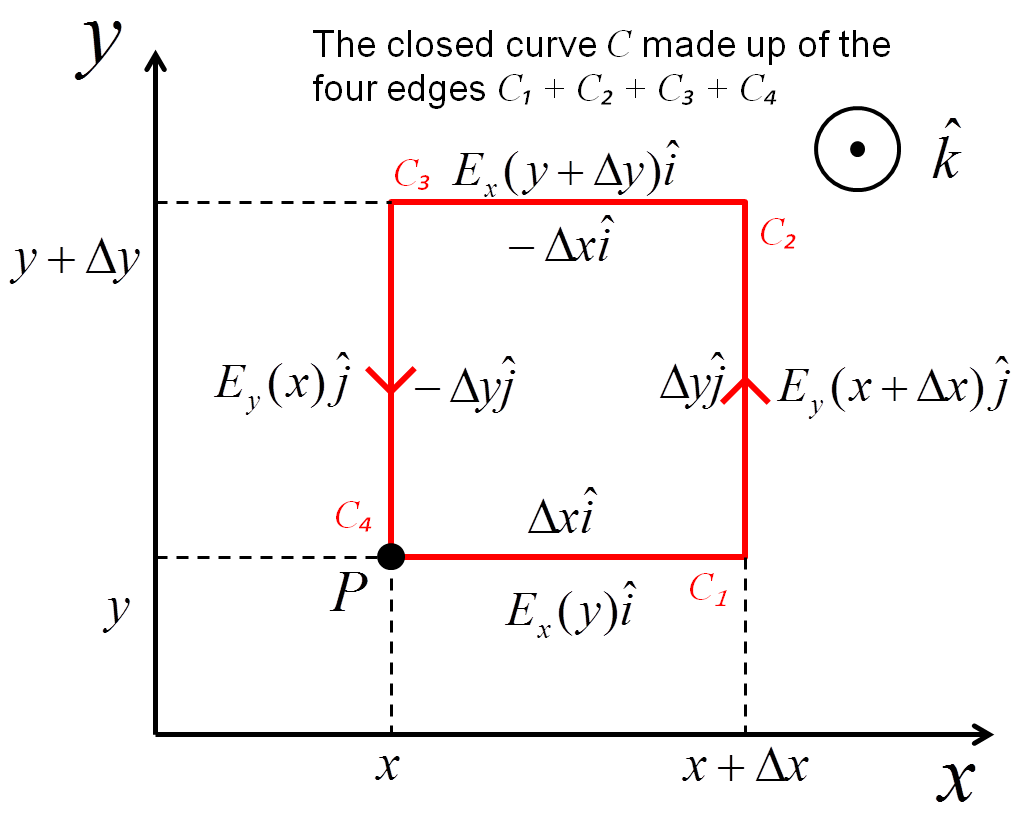
Consider a vector field \( \vec{E}(x,y,z) \), we want to measure the curl at the point \( P \) located at \( (x,y,z) \).
Let's focus on the \( \hat{k} \) component. A surface of area \( \Delta A = \Delta x \Delta y \) with a normal pointing in the \( \hat{k} \) direction is located within the field with one corner at \( P \). The circulation around the perimeter \( C \) of the surface can be broken down into four parts. The work done moving along each side of the square.
$$ \oint _C \vec{E} \circ d\hat{l} = \int_{C_1} E_x(y) \hat{i} \circ \hat{i} dx + \int_{C_2} E_y(x+\Delta x) \hat{j} \circ \hat{j} dy - \int_{C_3} E_x(y+\Delta y) \hat{i} \circ \hat{i} dx - \int_{C_4} E_y(x)\hat{j} \circ \hat{j}dy $$
$$ = \int_{C_1} E_x(y) dx + \int_{C_2} E_y(x+\Delta x) dy - \int_{C_3} E_x(y+\Delta y) dx - \int_{C_4} E_y(x)dy $$
|
|
|
As the surface is very small, we can say that \( E_x \) and \( E_y \) are constant along each side, therefore
$$ \oint _C \vec{E} \circ d\hat{l} = E_x(y)\Delta x + E_y(x+\Delta x)\Delta y - E_x(y+\Delta y)\Delta x - E_y(x) \Delta y $$
$$ = [E_x(y) - E_x(y+\Delta y)] \Delta x + [E_y(x+\Delta x) - E_y(x)] \Delta y $$
Let's insert this expression back into limit in the definition of curl
$$ \lim_{\Delta A \rightarrow 0} \frac{1}{\Delta A} \oint _C \vec{E} \circ d\vec{l} = \lim_{\Delta A \rightarrow 0} \frac{1}{\Delta x \Delta y} \big([E_x(y) - E_x(y+\Delta y)] \Delta x + [E_y(x+\Delta x) - E_y(x)] \Delta y \big)$$
$$ = \lim_{\Delta A \rightarrow 0} \Bigg[ \frac{E_x(y) - E_x(y+\Delta y)}{\Delta y} + \frac{E_y(x+\Delta x) - E_y(x)}{\Delta x} \Bigg]$$
As \( \Delta V \rightarrow 0 \), \( \Delta x \rightarrow 0 \) and \( \Delta y \rightarrow 0 \) therefore
$$ = \lim_{\Delta y \rightarrow 0} \Bigg[ \frac{E_x(y) - E_x(y+\Delta y)}{\Delta y} \Bigg] + \lim_{\Delta x \rightarrow 0} \Bigg[ \frac{E_y(x+\Delta x) - E_y(x)}{\Delta x} \Bigg] $$
$$ = -\frac{\partial E_x}{\partial y} + \frac{\partial E_y}{\partial x} $$
They are partial derivatives as \( E_x \) and \( E_y \) depend on \( x\), \( y \) and \(z\). If we repeat this for the \( \hat{i} \) and \( \hat{j} \) components we similarly get
$$ \mathrm{curl}(\vec{E})=\Bigg(\frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z}\Bigg)\hat{i} + \Bigg(\frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x}\Bigg)\hat{j} + \Bigg(\frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y}\Bigg)\hat{k} $$
You wouldn't notice this at first but this nasty expression can be reverse engineered to a cross product between \( \vec{\nabla} \) and the vector field \( \vec{E} \). This can be remembered using a determinant.
$$ \mathrm{curl} (\vec{E}) = \vec{\nabla} \times \vec{E} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_x & E_y & E_z \end{vmatrix} $$
|
|

|