Examples

1. Given \( \vec{E} = e^{xy}\hat{i} + \sin xy \hat{j} + \cos^2 zx \hat{k} \), find \( \mathrm{div} (\vec{E}) \).
2. Given \( \vec{F} = x\hat{i} + y\hat{j} + z\hat{k} \), find \( \mathrm{div} (\vec{F}) \).
3. Given \( \vec{B} = 2yz\hat{i} + x^2\hat{j} + \sin(e^y)\hat{k} \), find \( \mathrm{div}(\vec{B}) \).

4. Identify whether the vector fields \( \vec{E} \) shown below have divergence or not at the marked locations.

   

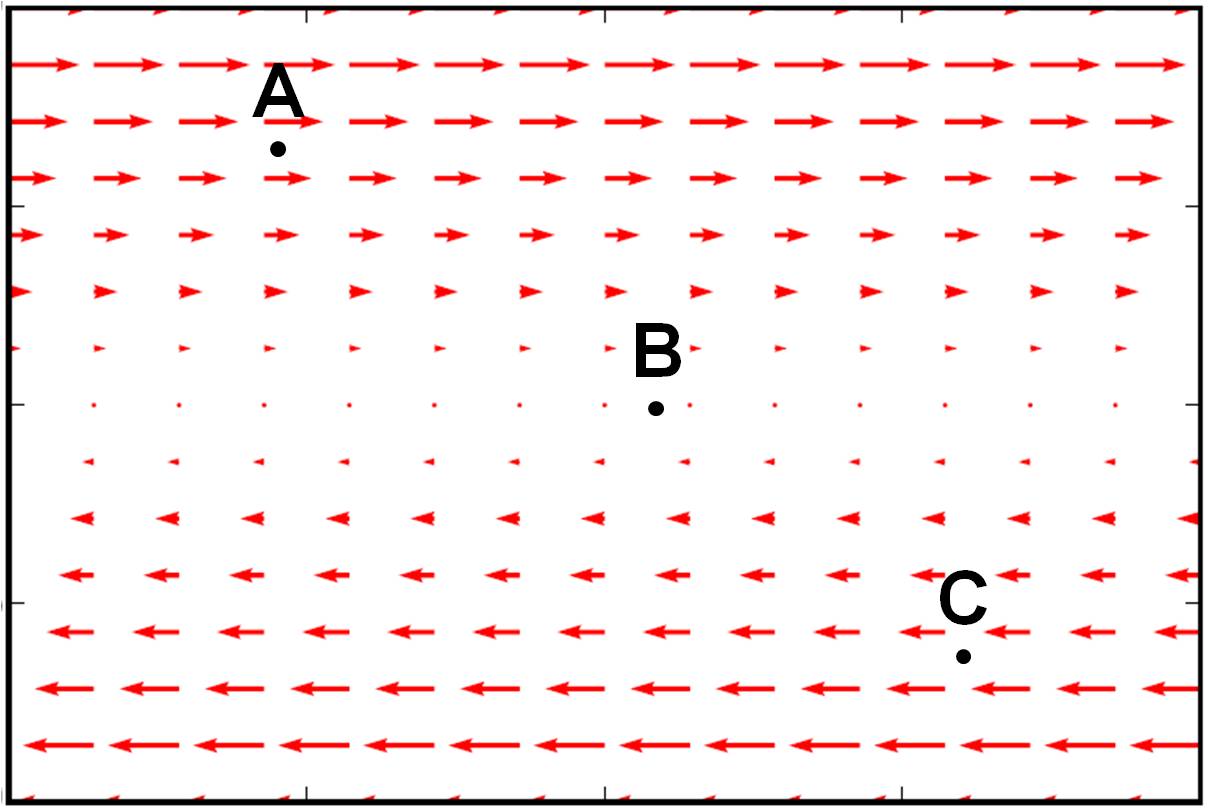
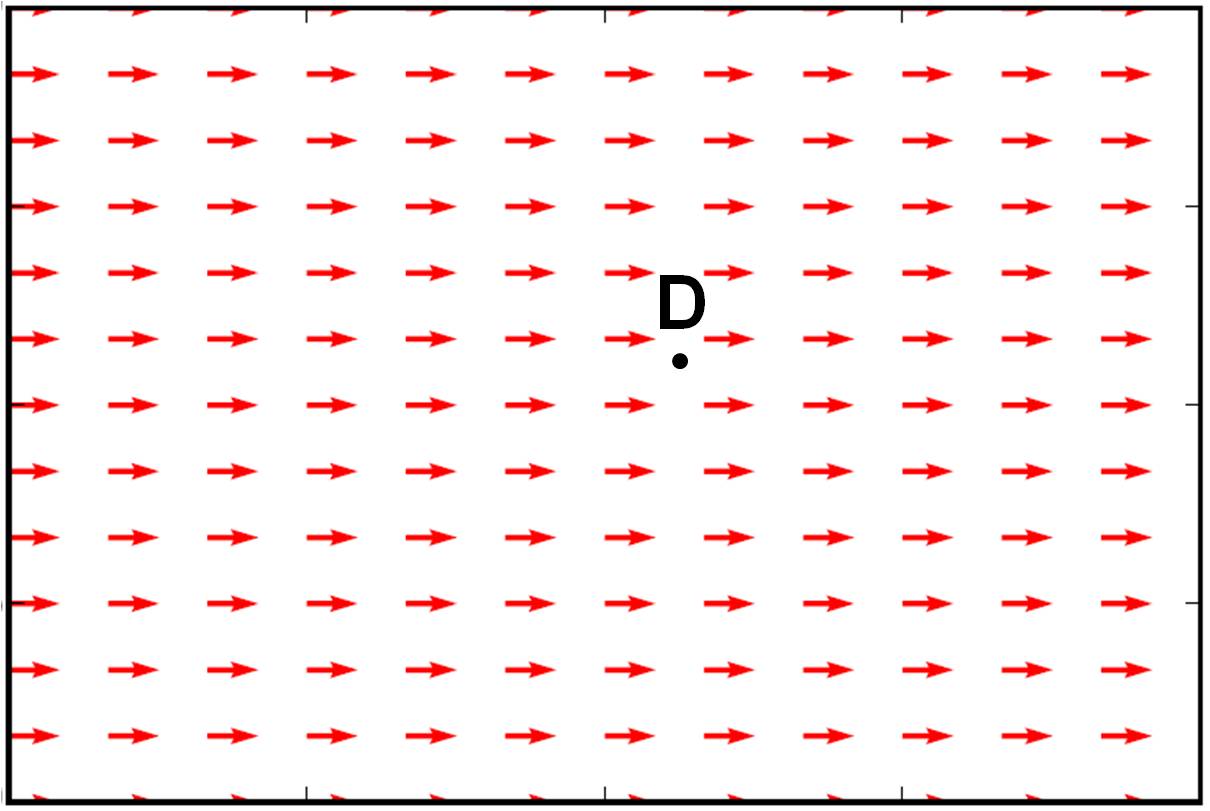
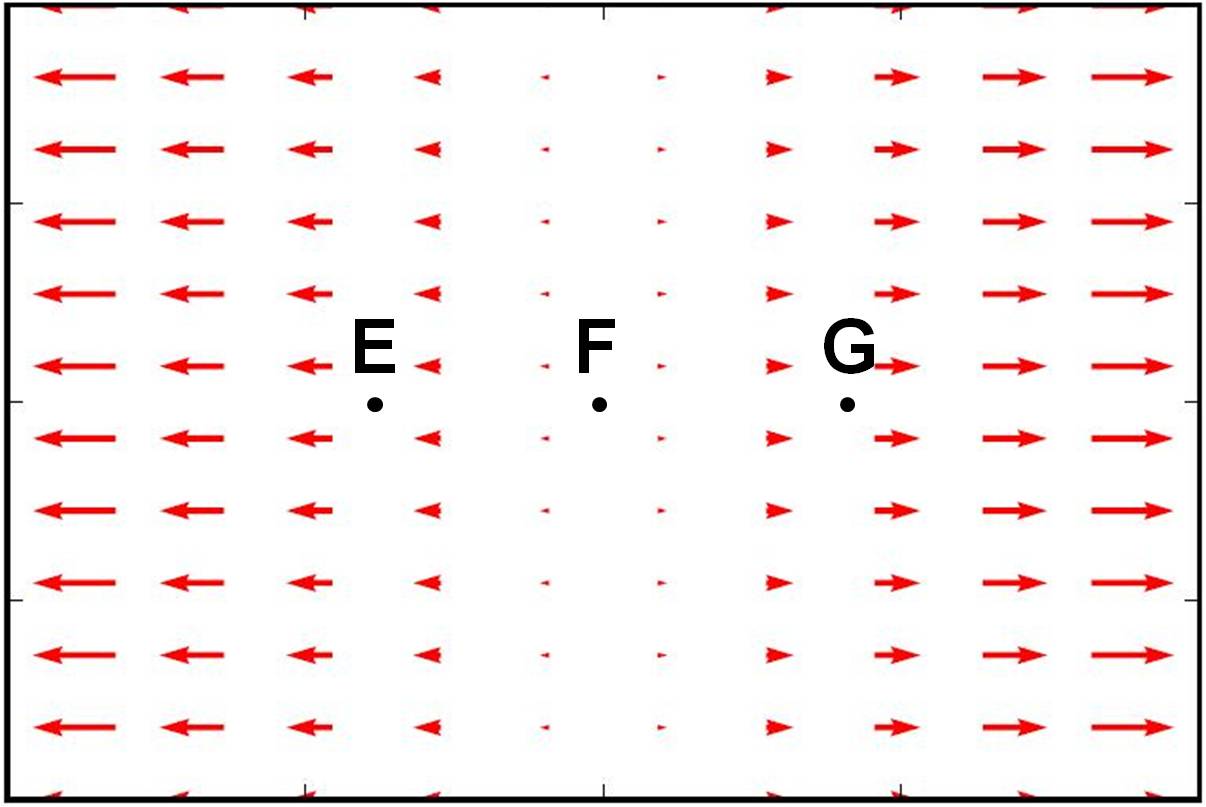
5. Calculate the charge density \( \rho(x,y,z) \) that produces the electric field \( \vec{E} = E_0 (x^3 \hat{i} + y^3 \hat{j} + z^3 \hat{k}) \).