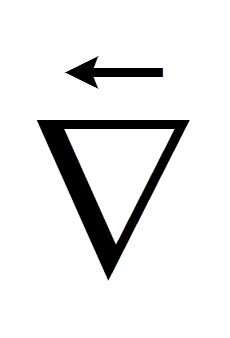All that derivation for divergence, it better be useful...
Yes, yes it is. Let's use our new expression for the divergence! The first of Maxwell's equations is Gauss' Law for electricity. Stated in integral form, it is the following: $$ \oint_S \vec{E} \circ \hat{n}dA = \frac{Q_{\mathrm{enc}}}{\varepsilon_0} $$
It states the flux through any closed surface \( S \) is proportional to the charge enclosed \( Q_{\mathrm{enc}} \) within this surface.
Here's our definition of divergence that we derived on the previous two pages.
$$ \vec{\nabla} \circ \vec{E} = \lim_{\Delta V \rightarrow 0} \frac{1}{\Delta V} \oint _S \vec{E} \circ \hat{n}dA. $$ Now let's insert Gauss' Law into the RHS of this definition $$ \vec{\nabla} \circ \vec{E} = \lim_{\Delta V \rightarrow 0} \frac{1}{\Delta V} \bigg(\frac{Q_{\mathrm{enc}}}{\varepsilon_0}\bigg)$$ We can bring out the constant from the limit $$ \vec{\nabla} \circ \vec{E} = \frac{1}{\varepsilon_0} \lim_{\Delta V \rightarrow 0} \frac{ Q_{\mathrm{enc}}}{\Delta V} $$ The quantity \( \frac{ Q_{\mathrm{enc}}}{\Delta V} \) is the charge density \( \rho \) within the volume \( \Delta V \). As the volume shrinks down to a point, it becomes the charge density at that point $$ \vec{\nabla} \circ \vec{E} = \frac{\rho(x,y,z)}{\varepsilon_0} $$This is Gauss' Law for electricity in differential form. It tells us that the divergence of the electric field \( \vec{E} \) at a location is proportional to the charge density \( \rho(x,y,z) \) at that location.
The same process can be applied to Gauss's Law for magnetic fields, transforming it from integral to differential form. $$ \oint_S \vec{B}\circ \vec{n}dA = 0 $$ $$ \downarrow \nonumber $$ $$ \vec{\nabla} \circ \vec{B} = 0 $$