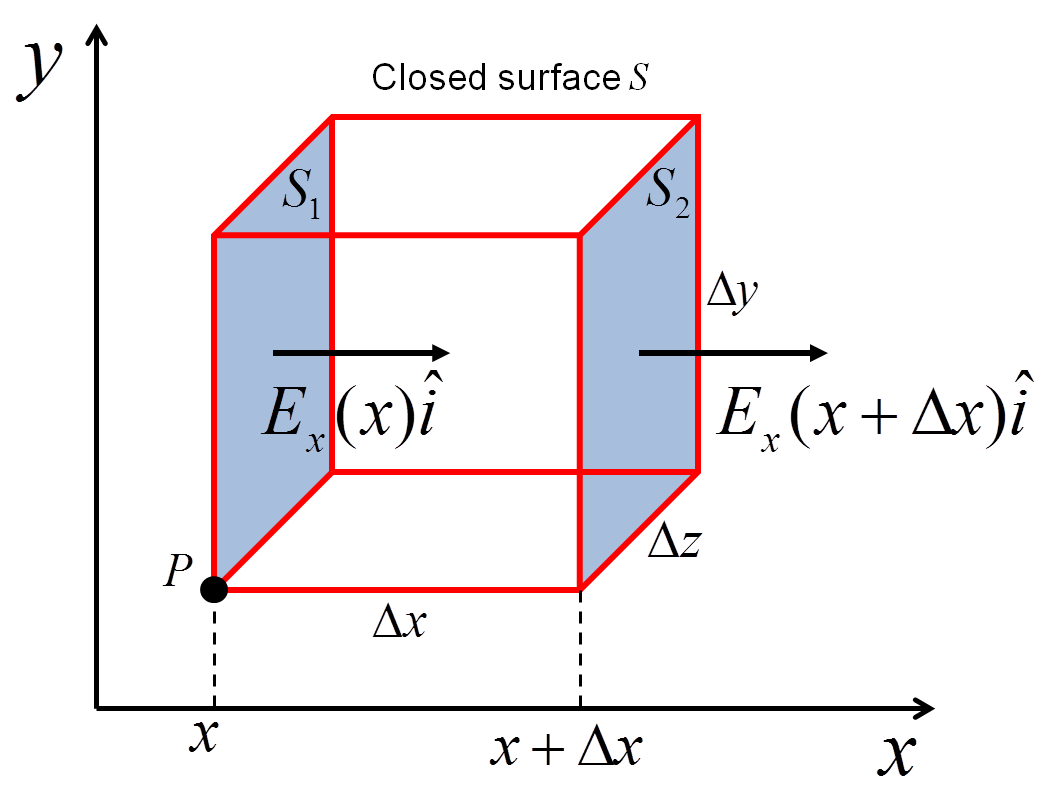
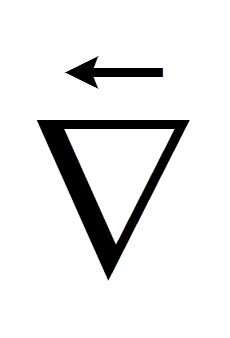Divergence Derivation

Divergence Derivation Here is the definition of divergence again, we need to use this to derive our operation! $$ \mathrm{div}(\vec{E}) \equiv \lim_{\Delta V \rightarrow 0} \frac{1}{\Delta V} \oint _S \vec{E} \circ \hat{n}dA. $$ Consider a vector field $ \vec{E}(x,y,z) = E_x \hat{i} + E_y \hat{j} + E_z \hat{k} $, we want to measure the divergence from the point $ P $ located at $ (x,y,z) $. A cube of volume $ \Delta V = \Delta x \Delta y \Delta z $ is located within the field with one corner at $ P $. The flux that leaves through this cube can be broken down into three parts, $ \Phi_x $, $ \Phi_y $ and $ \Phi_z $, which is the flux in the $ x $, $ y $ and $ z $ directions respectively. $$ \oint _S \vec{E} \circ \hat{n}dA = \Phi_x + \Phi_y + \Phi_z $$ If we substitute this back into our definition we get $$ \mathrm{div}(\vec{E}) \equiv \lim_{\Delta V \rightarrow 0} \frac{1}{\Delta V}(\Phi_x + \Phi_y + \Phi_z) $$ Let's focus on the $ x $ direction first. The flux in the $ x $ direction is the flux through the two surfaces $ S_1 $ and $ S_2 $. $$ \Phi_x = \int_{S_2} E_x \hat{i} \circ \hat{i} dA - \int_{S_1} E_x \hat{i} \circ \hat{i} dA $$ $$ = \int_{S_2} E_x dA - \int_{S_1} E_x dA $$

As the cube is very small, we can say that $ E_x $ is constant across each face. The flux in the $ x $ direction is $$ \Phi_x = E_x(x+ \Delta x )\Delta y \Delta z - E_x(x)\Delta y \Delta z $$ $$ \Phi_x = [E_x(x+ \Delta x ) - E_x(x)]\Delta y \Delta z $$ The flux through the left face is negative as the surface normal here points in the opposite direction to the right face. Let's multiply the top and bottom of equation (7) by $ \Delta x $ $$ \Phi_x = \frac{E_x(x+ \Delta x ) - E_x(x)}{\Delta x} \Delta x \Delta y \Delta z $$ If we substitute this back into the limit in our definition of divergence we get $$ \lim_{\Delta V \rightarrow 0} \frac{\Phi_x}{\Delta V} = \lim_{\Delta V \rightarrow 0} \frac{1}{\Delta x \Delta y \Delta z} \frac{E_x(x+ \Delta x ) - E_x(x)}{\Delta x} \Delta x \Delta y \Delta z $$ As $ \Delta V \rightarrow 0 $ all the sides of the cube shrink, therefore $ \Delta x \rightarrow 0 $ and the limit can be written as $$ = \lim_{\Delta x \rightarrow 0} \frac{E_x(x+ \Delta x ) - E_x(x)}{\Delta x} = \frac{\partial E_x}{\partial x} $$ It is a partial derivative as $ E_x $ depends on $ x$, $ y $ and $z$. If we repeat this in the $ y $ and $ z $ directions we get $$ \mathrm{div}\vec{E} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} $$ We can take this a bit further by reverse engineering this expression. We arrive at a very neat operation involving del. $$ \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} = \bigg( \frac{\partial}{\partial x}\hat{i} + \frac{\partial}{\partial y}\hat{j} + \frac{\partial}{\partial z}\hat{k} \bigg) \circ (E_x \hat{i} + E_y \hat{j} + E_z \hat{k}) = \vec{\nabla} \circ \vec{E} $$ $$ \mathrm{div}\vec{E} = \vec{\nabla} \circ \vec{E} $$