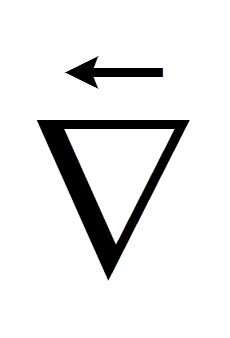Divergence

A vector field which you will all be familiar with is the electric field due to a point charge \(q\) as described by Coulomb's Law, $$ \vec{E} = \frac{1}{4\pi \varepsilon_0} \frac{q}{r^2} \hat{r} $$ This field points radially from the origin and the field lines diverge or converge at the charge depending on whether it is positive or negative respectively. A positive charge acts as a source of the field, creating an outward flow like a tap, and a negative charge acts like a sink into which the field drains away.

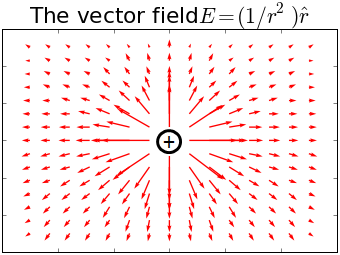
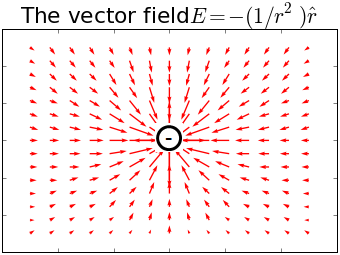
A tap/positive charge has positive divergence as it is a source. A drain/negative charge has a negative divergence as it is a sink.

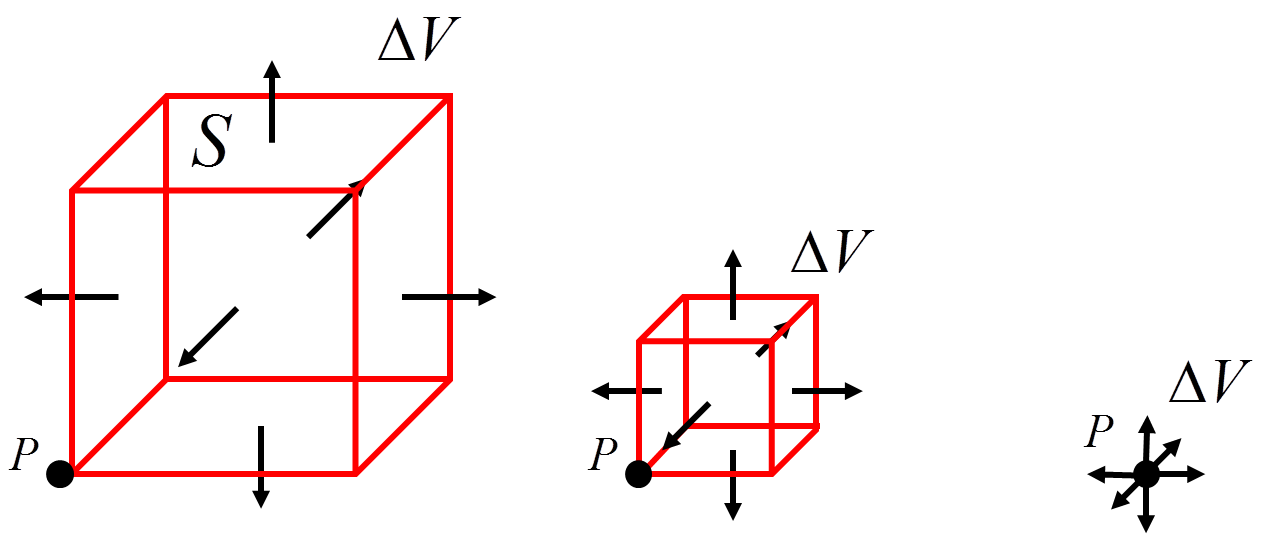
We need to derive an operation that takes a vector field \( \vec{E} \) and produces a scalar field \( \mathrm{div}(\vec{E}) \) which tells us how much the vector field lines converge or diverge from any point within the field.

We know from the previous page that flux tells us how much a vector field flows through an area in the field, but we want to work out the net flow from a point. How do we do this? We define the divergence as the ratio of the flux \( \Phi_E \) that leaves through a closed surface \( S \) to the volume \( \Delta V \) that this surface encloses. Then we let this volume shrink down to a point.