What the flux?

Before we can move onto the next operation with del we need to be introduced to the mathematical quantity called flux, which is Latin for flow. The flux of a vector field is a measure of how much a vector field flows through a surface. It a scalar quantity and is often given the symbol \( \Phi \).

If a flat surface of area \(A\) is perpendicular to a constant vector field \( \vec{E} \), i.e. its normal \( \hat{n} \) is parallel to the field: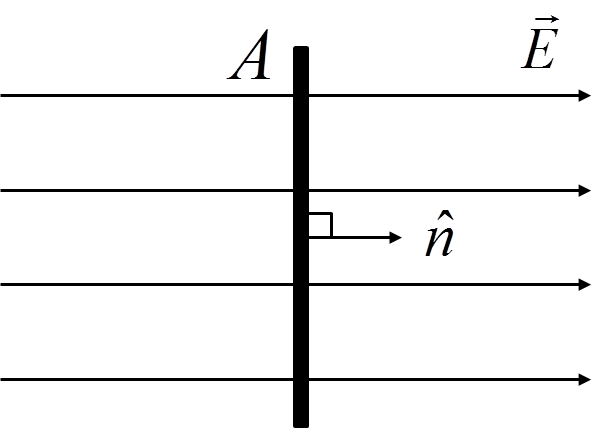
$$ \Phi_E = \vert \vec{E} \vert A $$
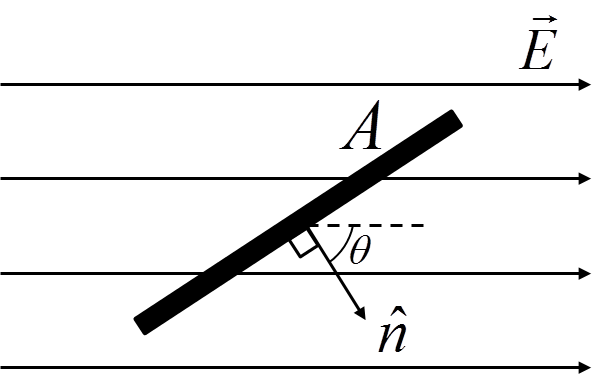If the surface normal is at an angle to a constant vector field:
$$ \Phi_E = \vert \vec{E} \vert A \cos\theta = \vec{E} \circ \hat{n} A $$
In general if the surface is curved and the vector field isn't uniform, we must consider a small infinitesimal amount of flux through an element of area \( dA \), $$ d\Phi_E = \vec{E} \circ \hat{n}dA \nonumber $$ Now let's add up all these infinitesimal fluxes to find the total flux through our curved surface in the non-uniform field, $$ \Phi_E = \int _S \vec{E} \circ \hat{n}dA $$

The subscript \( S \) reminds us that this is a surface integral across the surface \( S \) in question.

If we integrate across an entire closed surface such as a sphere, or a cube, we denote this with a closed integral \( \oint \) instead of \( \int \). A closed surface is anything which divides space into an inside and an outside.